概念

表达算法复杂度时候经常会看到O(n) O(1)等，这就是大O表示法，英文（Θ读做theta）

常见复杂度级别

  • Θ(1) 常数级别
  • Θ(log(n)) 对数级别(假设有一个有序数组, 以二分法查找)
  • Θ(n) 线性级别
  • Θ(n*log(n)) 线性对数级别
  • Θ(n^2) 平方级别
  • Θ(2^n) 指数级别

简化推导方法

算法执行的操作数去掉所有系数，去掉所有低阶项，只保留最高阶就是最终算法的复杂度。

示例1：

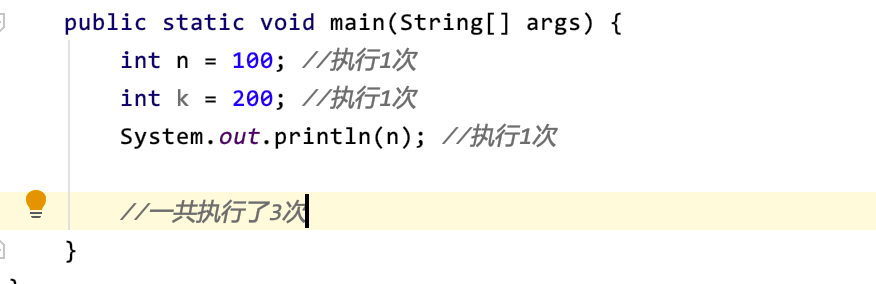
下图的示例代码一共执行了3次，没有低阶项，去掉系数3，则复杂度为Θ(1) O(1)复杂度

示例2：

下图的示例代码一共执行了2n+1次，去掉低阶项1，去掉系数2，则复杂度为Θ(n) O(1)复杂度

示例3：

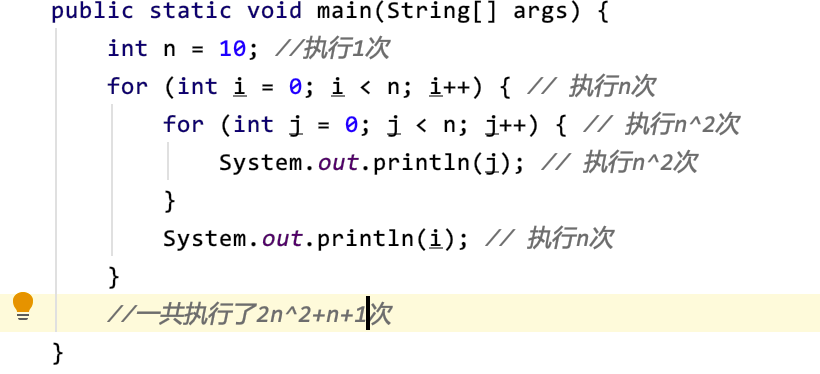
下图的示例代码一共执行了2n^2+n+1次，去掉低阶项1和n，去掉系数2，则复杂度为Θ(n^2) O(n^2)复杂度

操作数和复杂度对应

操作数 复杂度 名称
100 Θ(1) 常数
100logn+3 Θ(log(n)) 对数
3n+5 Θ(n) 线性
3n+5+100nlogn+3 Θ(n*log(n)) 线性对数
3n+5+ 7n^2 Θ(n^2) 平方
2^n Θ(2^n) 指数

性能

Θ(1)<Θ(log(n))<Θ(n)<Θ(n*log(n))<Θ(n^2)<Θ(2^n)